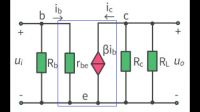
求大神帮帮忙!首先要看这个人和你是什么关系,你是女生,他是男生,你怕伤害他,那关系肯定不一般。一、如果是男朋友,那可以说的稍微直接一点没关系,毕竟他作为男朋友,需要互相包容对方
求大神解答
求大神解答
首先呢石同学中考失误的原因也许不是因为他的虚伪,在重大考试中试卷能测试出来的除了你平时的实力,还有你的心态,也许这位石同学只是在中考的时候心态不好也就是意志不坚定,导致考试没考好,根据你的描述可以看出石头学也许是一个心思细腻,比较圆滑也可以说成善于根据外部环境调整自己的人,可能这也导致他不是那么自信,比较受外部环境影响,中考是比较重要考试或许不是因为能力考砸,是因为心态,过于激进的特别想考好和特别觉得自己考不好都不是好的考试状态。其次你觉得自己表里不一,其实当你对自己某些行为有所察觉时,本身就证明其实你是比较正直善良的,你甚至对这些有些罪恶感,更加说明你意识到自己某些行为可能不恰当,这些是以后离散数学,求大神解答!
(1) 证明:
①R包含(a,a),(b,b),(c,c),(d,d),(e,e)所以R具有自反性;
②R包含(a,b),(a,c),(a,d),(a,e),(b,c),(b,e),(c,e),(d,e),没有(b,a),(c,a),(d,a),(e,a),(c,b),(e,b),(e,c),(e,d),所以R具有反对称性;
③R具有传递性
综上,(A,R)是偏序集
(2)
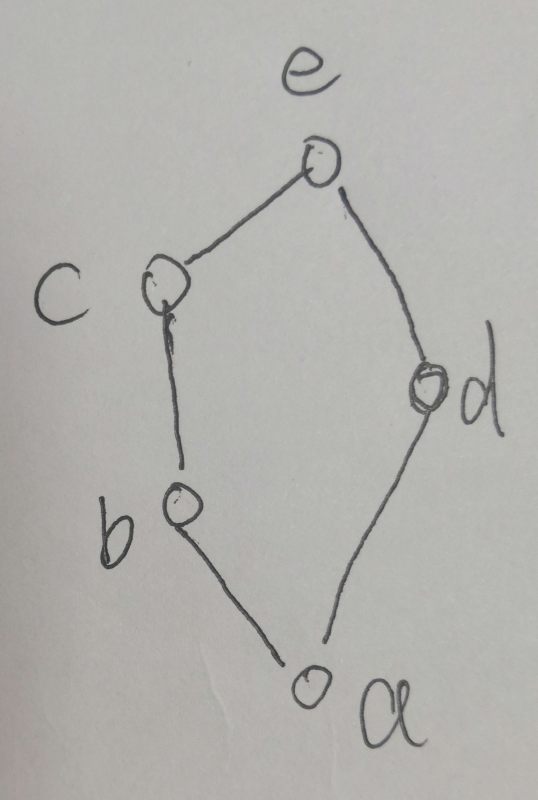
哈斯图
(3) 其最大元素是e,最小元素是a
(4)子集{a,b,c}的上界c,下界a,上确界c,下确界a
求大神解答,
报纸的用途
1、查看各种新闻信息,用手机就可以了,报纸可以拿来当废品卖。
2、报纸可以消化造纸厂的纸张。
3、可以维持印刷厂的产值。
4、报纸用来刊登过时的新闻和消息。
5、大爷大妈收集报纸去卖钱。
6、报纸上可以刊登广告。
7、不使用智能手机的大爷大妈看过时新闻使用。
8、报纸将慢慢走向消失,目前是一个短暂的过渡期。
9、在没有进入智能手机时代保存的报纸,以后会成为一种古董。

报纸的以及纸质文件
很多纸质的文件、合同、收据、书本、教材随着时代的进步,智能手机的全面普及,使用面会越来越窄,最终都会慢慢走向消失。
报纸的销售量会越来越少,目前大家还有使用纸质文件的习惯,这种习惯是有一定的惯性,但是人们应该有充分的理由相信在很短的周期内,报纸会基本消失。
如果家里有旧报纸可以进行二次使用,如长期不使用的碗盘、杯子在收藏前,可先用报纸将碗盘包起来,一来防止灰尘弄脏碗盘,二来再搬动或重新放置时,也比较不易破裂。
求大神解答!!
2、(1)——(4)分别是:CDBA
解析如下:
2. (1)假设α=π/4,可知:3π+α在第三象限,
则sin(π+α)为负数,即-sinα. 选 C.
(2)假设α=π/4,可知:2009π-α在第二象限,
先让2009π÷2-α=1004×2π+π-α,
则cos(π-α)为负数,即-cosα. 选 D.
(3)公式:sin(π/2+α)=cosα
假设α=π/4,可知:π/2+α在第二象限,
则sin(π/2+α)为负数,即cosα. 选 B.
(4)公式: cos(π/2-α)=sinα
假设α=π/4,可知:π/2-α在第一象限,
则cos(π/2-α)为正数,即sinα.选 A.
常用公式

公式一: 设α为任意角,终边相同的角的同一三角函数的值相等:
sin(2kπ+α)=sinα (k∈Z)
cos(2kπ+α)=cosα (k∈Z)
tan(2kπ+α)=tanα (k∈Z)
cot(2kπ+α)=cotα(k∈Z)
公式二: 设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:
sin(π+α)=-sinα
cos(π+α)=-cosα
tan(π+α)= tanα
cot(π+α)=cotα
公式三: 任意角α与-α的三角函数值之间的关系(利用 原函数 奇偶性):
sin(-α)=-sinα
cos(-α)= cosα
tan(-α)=-tanα
公式四: 利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:
sin(π-α)= sinα
cos(π-α)=-cosα
tan(π-α)=-tanα
cot(π-α)=-cotα
公式五: 利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:
sin(2π-α)=-sinα
cos(2π-α)= cosα
tan(2π-α)=-tanα
cot(2π-α)=-cotα
公式六: π/2±α与α的三角函数值之间的关系:
sin(π/2+α)=cosα
sin(π/2-α)=cosα
cos(π/2+α)=-sinα
cos(π/2-α)=sinα
tan(π/2+α)=-cotα
tan(π/2-α)=cotα
cot(π/2+α)=-tanα
cot(π/2-α)=tanα
推算公式:3π/2 ± α与α的三角函数值之间的关系:
sin(3π/2+α)=-cosα
sin(3π/2-α)=-cosα
cos(3π/2+α)=sinα
cos(3π/2-α)=-sinα
tan(3π/2+α)=-cotα
tan(3π/2-α)=cotα
cot(3π/2+α)=-tanα
cot(3π/2-α)=tanα
诱导公式记忆口诀:“奇变偶不变,符号看象限”。
“奇、偶”指的是π/2的倍数的奇偶,“
变与不变”指的是三角函数的名称的变化:
“变”是指正弦变余弦,正切变余切。
(反之亦然成立)“符号看象限”的含义是:把角α看做锐角,不考虑α角所在象限,
看n·(π/2)±α是第几象限角,从而得到等式右边是正号还是负号。
以cos(π/2+α)=-sinα为例,等式左边cos(π/2+α)中n=1,
所以右边符号为sinα,把α看成锐角,
所以π/2<(π/2+α)<π,y=cosx在区间(π/2,π)上小于零,
所以右边符号为负,所以右边为-sinα。
符号判断口诀:
全,S,T,C,正。这五个字口诀的意思就是说:
第一象限内任何一个角的四种三角函数值都是“+”;
第二象限内只有正弦是“+”,其余全部是“-”;
第三象限内只有正切是“+”,其余全部是“-”;
第四象限内只有余弦是“+”,其余全部是“-”。
也可以这样理解:一、二、三、四指的角所在象限。
全正、正弦、正切、余弦指的是对应象限三角函数为正值的名称。
口诀中未提及的都是负值。
“ASTC”反Z。意即为“all(全部)”、“sin”、“tan”、“cos”
按照将字母Z反过来写所占的象限对应的三角函数为正值。
另一种口诀:正弦一二切一三,余弦一四紧相连,言之为正。
公式与口诀来自于百度百科。
求大神解答?
Option Explicit
Public Sub Main()
QuadraticEquationRoot
End Sub
Public Sub QuadraticEquationRoot()
Dim a As Single, b As Single, c As Single, Discriminant As Single
a = InputCoefficients("a"): b = InputCoefficients("b"): c = InputCoefficients("c")
If a = 0 Then
MsgBox "数据错误!a不能为0"
Else
Discriminant = b ^ 2 - 4 * a * c
DisplayEquation a, b, c
If Discriminant >= 0 Then
RealRoot a, b, Discriminant
Else
ComplexRoot a, b, Discriminant
End If
Debug.Print
End If
End Sub
Public Function InputCoefficients(ByVal m)
InputCoefficients = InputBox(m & "=")
If Not IsNumeric(InputCoefficients) Then
MsgBox "数据错误!请重新输入", 16
InputCoefficients = InputCoefficients(m)
End If
End Function
Public Sub RealRoot(ByVal u As Single, ByVal v As Single, ByVal d As Single)
Dim p As Single, q As Single, x1 As Single, x2 As Single
p = (-v - Sqr(d)) / (2 * u): q = (-v + Sqr(d)) / (2 * u)
If p >= q Then
x1 = p: x2 = q
Else
x1 = q: x2 = p
End If
Debug.Print "x1=" & Format(Rounding(x1), "0.00") & Space(1) & "x2=" & Format(Rounding(x2), "0.00")
End Sub
Public Sub ComplexRoot(ByVal u As Single, ByVal v As Single, ByVal d As Single)
Dim m As Single, n As Single
m = -v / (2 * u): n = Sqr(-d) / (2 * u)
If n > 0 Then
If m = 0 Then
Debug.Print "x1=" & Format(Rounding(n), "0.00") & "i" & _
Space(1) & "x2=" & "-" & Format(Rounding(n), "0.00") & "i"
Else
Debug.Print "x1=" & Format(Rounding(m), "0.00") & "+" & Format(Rounding(n), "0.00") & "i" & _
Space(1) & "x2=" & Format(Rounding(m), "0.00") & "-" & Format(Rounding(n), "0.00") & "i"
End If
Else
If m = 0 Then
Debug.Print "x1=" & Format(Rounding(-n), "0.00") & "i" & _
Space(1) & "x2=" & "-" & Format(Rounding(-n), "0.00") & "i"
Else
Debug.Print "x1=" & Format(Rounding(m), "0.00") & "+" & Format(Rounding(-n), "0.00") & "i" & _
Space(1) & "x2=" & Format(Rounding(m), "0.00") & "-" & Format(Rounding(-n), "0.00") & "i"
End If
End If
End Sub
Public Function Rounding(ByVal Num As Single) As Single
Rounding = Int(Num * 100 + 0.5) / 100
End Function
Public Sub DisplayEquation(ByVal r As Single, ByVal s As Single, ByVal t As Single)
Dim rStr As String, sStr As String, tStr As String
rStr = CStr(r): sStr = (s): tStr = CStr(t)
Simplify rStr, sStr, tStr
If s = 0 And t = 0 Then
Debug.Print rStr & "x^2" & "=0"
ElseIf s = 0 Then
If t > 0 Then
Debug.Print rStr & "x^2" & "+" & tStr & "= 0"
Else
Debug.Print rStr & "x^2" & tStr & "=0"
End If
ElseIf t = 0 Then
If s > 0 Then
Debug.Print rStr & "x^2" & "+" & sStr & "x" & "=0"
Else
Debug.Print rStr & "x^2" & sStr & "x" & "=0"
End If
ElseIf s > 0 And t > 0 Then
Debug.Print rStr & "x^2" & "+" & sStr & "x+" & tStr & "=0"
ElseIf s < 0 And t > 0 Then
Debug.Print rStr & "x^2" & sStr & "x+" & tStr & "= 0"
ElseIf s > 0 And t < 0 Then
Debug.Print rStr & "x^2" & "+" & sStr & "x" & tStr & "=0"
Else
Debug.Print rStr & "x^2" & sStr & "x" & tStr & "=0"
End If
End Sub
Public Sub Simplify(ByRef strA As String, ByRef strB As String, ByRef strC As String)
If strA = "1" Then strA = ""
If strA = "-1" Then strA = "-"
If strB = "1" Then strB = ""
If strB = "-1" Then strB = "-"
End Sub

相关文章
- 详细阅读
-
求大神帮忙看看这配置玩DNF很卡的详细阅读

这电脑,系统也刚装过。玩DNF,感觉一卡一卡,卡顿。大神帮忙看看,哪里的毛病?网速也有关系的。可能是网络不好导致的。 外部问题: 1、网络环境差,可通过其他同网络内的机器确认是否有
-
有哪位大神知道图片的女生叫什么名详细阅读

谁知道图片里的女生叫什么名字?她叫沈芳芳,江西上饶的,这个妹子现在在江苏无锡上班,你要微博的话直接去新浪微博搜索她的名字就有了哪位大神知道这两个女生的名字,只有图片不知道
-
哪个大神有品茗的安全计算软件破解详细阅读

品茗软件破解版?我有品茗安全计算软件完美破解版,支持32和64位电脑系统,带有破解补丁,全功能使用你好,品茗安全计算软件破解版,能发一个吗?我有品茗安全计算软件完美破解版,带有破解
-
这款主机配置可以玩地下城与勇士(DN详细阅读

这个电脑主机配置值多少钱求大神指点,玩地下城与勇士卡吗?处理器240,主板120,内存170,固态硬盘170,显卡400,电源50,机箱100,显示器500。 虽然主板三件套有点老。但是运行和DNF一点问
-
学习动漫游戏专业的学生需要对电脑详细阅读

学习动漫游戏专业的学生需要对电脑有一定的基础吗?学习动漫游戏专业需要有一定的计算机基础,而且基础不低,需要熟练掌握各种软件,动漫设计分为:2D动漫软件,3D动漫软件和网页动漫软
-
软件专业主要学习什么?详细阅读

软件技术主要学什么?软件技术主要学习以下内容:1、编程语言课程(包括Microsoft公司Windows平台开发技术和SUN公司(已被甲骨文收购)的Java开发技术)2、支撑课程(如数据库技术、网
-
学习电脑技术大概要多少费用啊?详细阅读

想报一个电脑培训班要多少钱?电脑培训从3000元—30000元不等,电脑培训班要多少钱与培训课程专业和学员自身有关,主要是专业和时间。具体分析如下: 1、初级电脑培训班:初级电脑培
-
请问我在大塔儿巷老年大学电脑学习详细阅读

在培训班交了学费没有去学习,可以要求退吗?如果被拒绝怎么办正规培训学校是可以在规定时间内可退,过了视情况可以协商,能退不退可到当地劳动和社会保障局投诉。 深圳正规职业技
-
玩个魔域 数组成员引用下标超出定详细阅读

运行时错误:数组成员引用下标超出定义范围,求大神帮助小小修改了下,测试可以 .版本 2 .支持库 shell .程序集 窗口程序集1 .程序集变量 关机时间, 文本型, , "2" .子程序 _时钟