关于c语言编程的bug这时很正常的问题.打代码没有bug才不正常.但是编译时的错误还是比较容易避免的,常见的可以通过以下几种方法解决
语法错误:比如说变量名打错,少一个分号,
显式与显示的区别?
什么叫显式?什么叫隐式?
显式算法基于动力学方程,分为静态显式算法和动态显式算法。显式算法最大优点是有较好的稳定性。动态显式算法采用动力学方程的一些差分格式(如广泛使用的中心差分法、线性加速度法、Newmark法和wilson法等),不用直接求解切线刚度,不需要进行平衡迭代。
隐式算法中,在每一增量步内都需要对静态平衡方程进行迭代求解,并且每次迭代都需要求解大型的线性方程组,这以过程需要占用相当数量的计算资源、磁盘空间和内存。
该算法中的增量步可以比较大,至少可以比显式算法大得多,但是实际运算中上要受到迭代次数及非线性程度的限制,需要取一个合理值。

特别注意
一、“差分法”本身是一种“精算法”而非“估算法”,得出来的大小关系是精确的关系而非粗略的关系;
二、“差分法”与“化同法”经常联系在一起使用,“化同法紧接差分法”与“差分法紧接化同法”是资料分析速算当中经常遇到的两种情形。
三、“差分法”得到“差分数”与“小分数”做比较的时候,还经常需要用到“直除法”。
四、如果两个分数相隔非常近,我们甚至需要反复运用两次“差分法”,这种情况相对比较复杂,但如果运用熟练,同样可以大幅度简化计算。
C++ 隐式和显式的区别
隐式实现和显示实现的例子 隐式地实现接口成员 创建一个接口,Chinese,包含一个成员 Speak;我们创建一个类Speaker,实现接口Chinese //隐藏式实现例子 public interface Chinese { string Speak(); } public class Speaker : Chinese { public string Speak() { return "中文"; } } 这个就是隐式实现 显式地实现接口成员 -- 创建一个仅通过该接口调用并且特定于该接口的类成员。这是使用接口名称和一个句点命名该类成员来实现的。 创建一个接口,English,包含一个成员C语言 显式 隐式是什么意思
隐式转换就是不带转换类型的转换,如int转float你可以这样子float a ;int b = 4; a=b就是隐式转换,而a = (float)b就是显示转换。区别在于当向下转换时如果不显示转换就会有问题,如float a = 4.5; int b = a;这里就可能报错,因为int可以自动上升为float,但由float不能自动转化为int,这里就需要显式转换,即int b = (float)a才是最保险的;所以显式转换肯定不会出错,但隐式转换就说不定了。什么是显式解,什么是隐式解
方程的解可以写出y=f(x)的叫显式解,只能写出f(x,y)=C的叫隐式解。
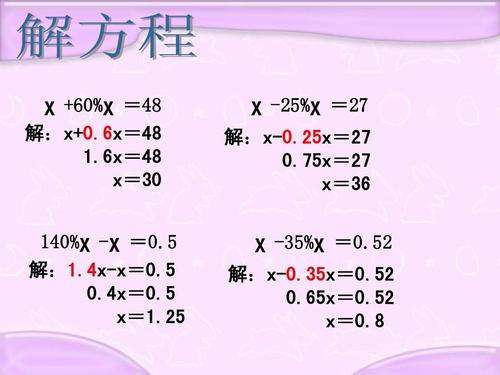
方程是指含有未知数的等式。是表示两个数学式(如两个数、函数、量、运算)之间相等关系的一种等式,使等式成立的未知数的值称为“解”或“根”。求方程的解的过程称为“解方程”。
通过方程求解可以免去逆向思考的不易,直接正向列出含有欲求解的量的等式即可。方程具有多种形式,如一元一次方程、二元一次方程、一元二次方程等等,还可组成方程组求解多个未知数。
扩展资料
1、未知数:通常设x.y.z为未知数,也可以设别的字母,全部小写字母都可以。
2、“次”:方程中次的概念和整式的“次”的概念相似。指的是含有未知数的项中,未知数次数最高的项。而次数最高的项,就是方程的次数。
3、“解”:方程的解,指使,方程的根是方程两边相等的未知数的值,指一元方程的解,两者通常可以通用。
4、解方程:求出方程的解的过程,也可以说是求方程中未知数的值的过程,或说明方程无解的过程叫解方程。
5、方程中,恒等式叫做恒等方程,矛盾式叫做矛盾方程。在未知数等于某特定值时,恰能使等号两边的值相等者称为条件方程,例如 ,在 时等号成立。使方程左右两边相等的未知数的值叫做方程的解。
参考资料来源:百度百科——隐式解
参考资料来源:百度百科——方程
显式接口和隐式接口的区别
隐式实现和显示实现的例子 隐式地实现接口成员 创建一个接口,Chinese,包含一个成员 Speak;我们创建一个类Speaker,实现接口Chinese //隐藏式实现例子 public interface Chinese { string Speak(); } public class Speaker : Chinese { public string Speak() { return "中文"; } } 这个就是隐式实现 显式地实现接口成员 -- 创建一个仅通过该接口调用并且特定于该接口的类成员。这是使用接口名称和一个句点命名该类成员来实现的。 创建一个接口,English,包含一个成员相关文章
-
为什么C++这个出了什么BUG详细阅读

-
零基础的小白学那个编程语言,最容易详细阅读

零基础入门学习什么编程语言比较好如果你想学习编程,虽然选择第一门编程语言与你想用它来做什么最终达到什么目的有很大的关系,但是事实上某些编程语言的确比其他语言要好学。
-
C++问题王国比赛(kingdom),在线等,急详细阅读

王国kingdom游戏闪退怎么办 闪退跳出的解决办法你好, 解决办法: 1、英文目录,游戏是否在纯英文路径下运行,比如这样D:\Kingdom。要保证游戏所在目录下没有奇怪的字符。(这个可以
-
C++如何实现C53最简单方法详细阅读

排列组合C(5,3)怎么计算写在纸上一步一步写把公式写出来。还有排列组合的A和C和P是怎么回事呢等于5×4×3(一共乘了三个数,等于上边数字的数量),然后再除以3×2×1(上边数的阶乘)
-
c++语言算法详细阅读

C语言基本算法1.输入语句:scanf("控制格式",接受值列表),其中控制格式常用的有:%d,%c,%s,%f,分别 表示整型,字符型,字符串和浮点型. 例如int a;char c;scanf("%d %c",&a,&c)
-
【c++】用while语句输出a和b范围内详细阅读

c语言中用while语句 输入俩个正整数显示他们之间所有整数的和,这段那错了 ?求解 谢谢!#include void main() { int a, b; int m, n; scanf("%d%d", &a, &b); if (a < b) m = b
- 详细阅读
-
信息技术会考操作题photon已经做完详细阅读

信息技术学业水平考试步骤错了会不会影响成绩?不会,这种考试一是看你的最终结果,最终结果相同应该就能获得分数,步骤错了也分步骤顺序错了和步骤的具体操作错了,顺序错了不会有影
-
c++使用网上的代码报错详细阅读

为什么网上下的C语言程序都不能正常使用我最近学习C网上下的C语言程序都不能正常使用,一般有这些原因:硬件平台相关:如果你下的是硬件平台相关的代码,特别是单片机的C语言程序,代
-
我想学习编程,想下载个C++6.0,求个官详细阅读

初学c语言,谁能给个vc++6.0软件免费下载地址啊VC++6.0压缩文件直接给你了!
祝你学业有成!求C语言编程软件的下载地址,急!!!Visual C++ V6.0 sp6 简体中文版http://www.ddooo.com/s

