如何通过固有频率和阻尼比描述二阶系统特征?

二阶系统的阻尼比ζ和固有频率ωn对二阶系统主要有什么影响

二阶系统阻尼比ζ越小，上升时间tr则越小；ζ越大则tr越大。固有频率ωn越大，tr越小，反之则tr越大。固有频率具有角速度的量纲，而阻尼比为无量纲参量。

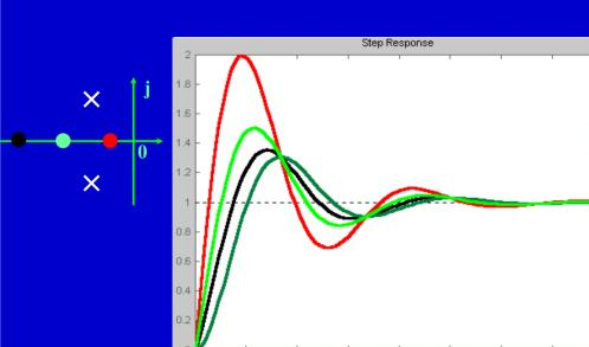
系统的行为由上定义的两个参量——固有频率ωn和阻尼比ζ所决定。

当ζ =1时，γ的解为一对重实根，此时系统的阻尼形式称为临界阻尼。

当ζ>1时，γ的解为一对互异实根，此时系统的阻尼形式称为过阻尼。

当0<ζ <1时，γ的解为一对共轭虚根，此时系统的阻尼形式称为欠阻尼。在欠阻尼的情况下，系统将以圆频率相对平衡位置作往复振动。

扩展资料：

模态阻尼准确的来讲是模态阻尼比，定义成每阶模态下与临界阻尼的比率。模态阻尼一般的模态测试中可以直接测试得到，一般从0.01到高阻尼系统的0.15或者更高。

与质量矩阵成正比的部分当频率趋于零时，变得无穷大，随着频率的增加而迅速变小；与刚度矩阵成正比的部分，则随着频率的增加而线性增加。

参考资料来源：

百度百科-二阶系统

2.二阶系统的阻尼比ξ取不同值时,其振荡特性有何特点？

阻尼振动是指，由于振动系统受到摩擦和介质阻力或其他能耗而使振幅随时间逐渐衰减的振动，又称减幅振动、衰减振动。[1]不论是弹簧振子还是单摆由于外界的摩擦和介质阻力总是存在，在振动过程中要不断克服外界阻力做功，消耗能量，振幅就会逐渐减小，经过一段时间，振动就会完全停下来。这种振幅随时间减小的振动称为阻尼振动．因为振幅与振动的能量有关，阻尼振动也就是能量不断减少的振动．阻尼振动是非简谐运动．阻尼振动系统属于耗散系统。这里的阻尼是指任何振动系统在振动中，由于外界作用或系统本身固有的原因引起的振动幅度逐渐下降的特性，以及此一特性的量化表征。

摩擦阻尼

由于摩擦阻力(包括介质粘滞阻力)使振动系统的能量逐渐转变为热运动能量，常称为摩擦阻尼。[1]例如单摆摆动的过程中振幅减小或停下来就是由于系统的阻力作用使摆的机械能转化为空气的内能．

辐射阻尼

由于振动系统引起周围介质的振动，使系统的能量转变为波动的能量向四周辐射出去，常称为辐射阻尼。[1]例如：琴弦发出声音不仅因为有空气的阻力要消耗能量，同时也因为以波的形式辐射而减少能量。最后琴弦会停止振动。

当阻尼很小时，在一段不太长的时间看不出振幅有明显的减小，就可以把它当作简谐运动来处理．

如图，以液体中的弹簧振子为例，介绍阻尼振动的动力学方程。[2]

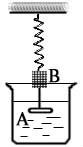
假设：振动速度较小时，摩擦力正比于质点的速率。即：

对物块应用牛顿第二定律：

为二阶线性常系数齐次方程，即阻尼振动的动力学方程。

振动方程

编辑

上述⑴式方程的特征根：

阻尼振动的微分方程有三种不同形式的解，具体如下。

欠阻尼

即：

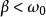
，则 ：

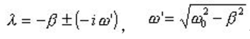
解为：

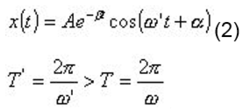
说明振动变慢（由于阻力作用）

振幅为

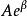
随时间的推移，

呈指数递减， 越大，振动衰减越快；

越小，振幅衰减越慢。

定义：

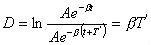
表示阻尼大小的标志，称对数减缩，即经过一个周期后，振幅的衰减系数。

过阻尼

即：

，则方程的解为：

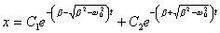
⑶

其中：

、

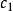
由初始条件决定。

随时间的推移，质点坐标单调地趋于零。质点运动是非周期的，甚至不是往复的。将质点移开平衡位置后释放，质点便慢慢回到平衡位置停下来，即过阻尼状态。

临界阻尼

即：

，则方程的解为：

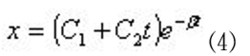
其中：

、

由初始条件决定。

此种状态，质点仍不往复运动。由于阻力较前者小，质点移开平衡位置释放后，质点很快回到平衡位置并停下来。 如图示。

应用

例如：天平的指针最好处于临界阻尼状态。（理想）

电流表、电压表的指针最好处于临界阻尼状态，有时处于欠阻尼状态。

希望我能帮助你解疑释惑。

二阶系统中,两个重要参量是什么?分别是如何影响系统的

二阶系统中，两个重要参量是系统响应时间和峰值时间变短，分别是影响系统的：

二阶系统阻尼比ζ越小，上升时间tr则越小；ζ越大则tr越大。固有频率ωn越大，tr越小，反之则tr越大。固有频率具有角速度的量纲，而阻尼比为无量纲参量。系统的行为由上定义的两个参量——固有频率ωn和阻尼比ζ所决定。

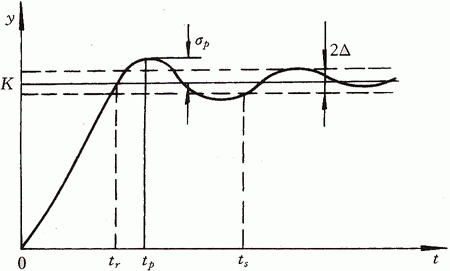
性能指标

控制系统动态特性的优劣，是通过动态特性性能指标来评价的。控制系统动态特性的性能指标通常是按系统的单位阶跃响应的某些特征量来定义的。多数控制系统的动态过程都具有振荡特性。因此我们选择欠阻尼振荡过程为典型代表，来定义动态特性的性能指标，并用这些指标来描述控制系统的动态过程品质。

二阶欠阻尼系统的无阻尼固有频率和阻尼固有频率有什么关系？

wd=wn*sqrt(1-xi^2)

其中，wd为有阻尼频率

wn为无阻尼频率

xi为阻尼比

在自动化领域，所谓欠阻尼，说明阻尼不够大，因此这个阻尼并不足以阻止振动越过平衡位置，此时系统将做振幅逐渐减小的周期性阻尼振动。系统的运动被不断阻碍，所以振幅减衰，并且振动周期也是越来越长，经过较长时间后，振动停止。

扩展资料：

任何一个振动系统，当阻尼增加到一定程度时，物体的运动是非周期性的，物体振动连一次都不能完成，只是慢慢地回到平衡位置就停止了。

一个系统受初扰动后不再受外界激励，因受到阻力造成能量损失而位移峰值渐减的振动称为阻尼振动。系统的状态由阻尼率ζ来划分。不同系统中ζ的计算式不同，但意义一样。

参考资料来源：百度百科--欠阻尼

《测试技术》一阶 二阶系统的动态特性指标是什么及他的合理取值范围?对系统有何影响?

时间常数 是一阶系统的重要特征参数。 越小，系统极点越远离虚轴，过渡过程越快。二阶系统的动态特性指标是固有频率 和阻尼比ζ

标签：理工学科 系统 自然科学 数学 学习