首页 > 软件 > 函数在某点的切线如何定义的？可以通过什么方法求解呢？

函数在某点的切线如何定义的？可以通过什么方法求解呢？

软件 2023-11-05

函数切线的具体定义是什么？

切线指的是一条刚好触碰到曲线上某一点的直线。更准确地说，当切线经过曲线上的某点（即切点）时，切线的方向与曲线上该点的方向是相同的，此时，“切线在切点附近的部分”最接近“曲线在切点附近的部分”（无限逼近思想）。tangent在拉丁语中就是“to touch”的意思。类似的概念也可以推广到平面相切等概念中.

函数的切线怎么求？

f(x)过(x0,y0)的切线当(x0,y0)在f(x)上时，由切线的斜率是f'(x0),所以方程是(y-y0)/(x-x0)=f'(x0) 当(x0,y0)不在f(x)上时，设切点是（x1,y1), 方程为(y-y0)/(x-x0)=f'(x1) y1=f(x1) (y1-y0)/(x1-x0)=f'(x1)由这两个方程可解出（x1，y1）就可求出方程

怎样求函数在一个点处的切线方程

如函数的倒数为：y=2x-2

所以点(0,3)斜率为：k=2x-2=-2

所以切线方程为：y-3=-2(x-0) （点斜式）

即2x+y-3=0

所以y=x^2-2x-3在(0,3)的切线方程为2x+y-3=0。

扩展资料

分析-解析法求切线方程

设圆上一点A为：

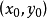
则有：

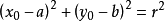
对隐函数求导，则有：

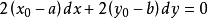
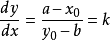
（隐函数求导法亦可证明椭圆的切线方程，方法相同）

或直接：

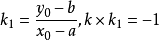
（k1为与切线垂直的半径斜率。）

得：

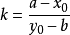
（以上处理是假设斜率存在，在后面讨论斜率不存在的情况）

所以切线方程可写为：

一个函数方程的切线方程怎么求？求详解

解：函数的切线方程就是去该函数的导数。例：y=ax²+bx+c(y为x的函数)上面一个点（m,n)
切线斜率k=y'=2ax+b，则过（a,b)点的切线方程为y-n=(2am+b)(x-m)。

数学：

数学是研究数量、结构、变化、空间以及信息等概念的一门学科。数学是人类对事物的抽象结构与模式进行严格描述的一种通用手段，可以应用于现实世界的任何问题，所有的数学对象本质上都是人为定义的。从这个意义上，数学属于形式科学，而不是自然科学。不同的数学家和哲学家对数学的确切范围和定义有一系列的看法。

怎么求一个函数在一个点上的切线

首先求函数的导数，把这个点的横坐标代入到导函数里得到切线方程的斜率，然后直线又过这个点，因此可以直接求出切线方程。

标签：函数数学学习自然科学高等数学（大学课程）

微信客服打电话核对关联的微信号是什么意思呢返回列表

大明白知识网 Copyright © 2020-2022 www.wangpan131.com. Some Rights Reserved. 京ICP备11019930号-18