函数形参 引用和指针有什么区别关于指针和引用的区别,首先要了解变量声明的实质。先看一个代码inta=10;该语句其实是在栈上分配了一块内存空间,整数类变量占用4字节,所以这句代
复变函数球函数的部分展开式 积极急急急急急急
复变函数求洛朗级数怎样分解函数式
复变函数求洛朗级数怎样分解函数式 尽量将分母化成熟悉的公式及它们对应(公式成立)的范围。 你要非常熟悉并掌握以下复变函数的洛朗展开式: (洛朗展开与泰勒展开的区别就在于展开区间:泰勒展开的展开区间无穷大,洛朗展开区间则有限。) ∑z^n=1/(z-1) (|z|<1), ∑z^n/n!=e^n (|z|<∞), sin z=∑(-1)^n•z^(2n+1) ∕ (2n+1)! (|z|<∞), cos z=∑(-1)^n•z^(2n) ∕ (2n)! (|z|<∞).复变函数级数展开问题?
分享解法如下。设f(z)=1/[(z-2)(1+z²)]=a/(z-2)+(bz+c)/(1+z²)。可求得a=1/5,b=-1/5,c=-2/5。∴f(z)=(1/5)[1/(z-2)-z/(1+z²)-2/(1+z²)]。 当1<丨z丨<2时,有丨z/2丨<1,丨1/z²丨<1。∴f(z)=(1/5)[(-1/2)/(1-z/2)-(1/z)/(1+1/z²)-(2/z²)/(1+1/z²)]。 此时,1/(1-z/2)=∑(z/2)^n,1/(1+1/z²)=∑(-1/z²)^n,n=0,1,2,……,∞。 ∴f(z)=(-1/10)∑(z/2)^n-(1/5)∑[(-1)^n][1/z复变函数 关于泰勒展开式的问题
第二种错了 因为泰勒展开只有正次幂 第二种是Laurent展开,含负次幂(主要部分) 在用1/(1-x)型展开公式时,首先就要注意收敛域(-1,1),所以1是|z+1| 3的区域展开复变函数 将函数f(z)=1/(z(z-1)) 展开成洛朗级数(1)1<|z|<正无穷
第一,确定展开点。这一题是z=1,如果没有特殊声明,就默认为z=0.
第二,找出函数的奇点,进而确定收敛圆环域。
函数的奇点为z=1,z=2。根据奇点和展开点之间的位置关系,可以将圆环域分为0<|z-1|<1和|z-1|>1两种情形。
作为实变函数,它是处处无穷可微的;但作为一个复变函数,在x= 0处不可微。用−1/x替换指数函数的幂级数展开式中的x,我们得到其洛朗级数,对于除了奇点X= 0以外的所有复数,它都收敛并等于ƒ(x)。
扩展资料:
解析函数是复变函数中一类具有解析性质的函数,复变函数论主要就是研究复数域上的解析函数。
共轭解析函数是和解析函数完全对称的一类函数,这使得复变函数变得完美,众人皆知对称是科学的一个普遍的美。
再者由于有了共轭解析函数类的提出,解析函数与共轭解析函数的不同组合才形成了复调和函数、双解析函数、多解析函数及相应的微分方程、积分方程等一系列新的数学分支的产生。
参考资料来源:百度百科--复变函数
复变函数,怎么展开成泰勒级数?刚学,不会做……
题号 一 二 三 四 五 六 总分 分数 一(每小题5分)试求下列各式的值(1) (2) (3) (4) (5) 二 (10分)设三点适合条件:,证明: 是内接于单位圆的一个正三角形的顶点三(每小题5分)下列函数在复平面上何处可导?何处解析? (1) (2)四计算下列积分值(1)(10分)计算积分,其中积分路径为:自原点到的直线段。圆周(2)(15分)求积分的值,其中为,。(3)(10分)五(10分)将函数展开为的泰勒展开式或洛朗展开式。六(10分)已知函数求函数在复平面上所有奇点处的留数之和。求积分标签:高等数学(大学课程) 大学课程 高等教育 数学 函数
相关文章
- 详细阅读
-
excel函数条件函数怎么写详细阅读

Excel中如何设置条件函数?IF函数的逻辑式是: IF(logical_test,value_if_true,value_if_false)其中,Logical_test 表示计算结果为 TRUE 或 FALSE 的任意值或表达式。
D1 公式为 -
excel函数计算加班时间详细阅读

Excel如何通过函数计算加班天数?公式为:=SUMIF(A$2:A$4,A6,C$2:C$4)+SUMIF(B$2:B$4,A6,C$2:C$4)excel函数计算加班时间举例说明。例如有数据表如图:第一步:在E2输入公式:=ROUND((
-
c语言,在主函数中输入一个正整数在详细阅读

C语言:输入一个正整数, 计算并显示出该数的各位数字之和.代码:
#include
intsum(intn){
ints=0;
while(n>0){
s+=n%10;
n/=10;
}
returns;
}
intmain(){
intn;
pr -
excel通用if函数判断时,条件区域空详细阅读

excel 如何让条件中的空格为空时,不显示计算结果。1、打开需要设置的excel表格,点击左上角的“文件”,如下图所示:2、选择最底部的“选项”,如下图所示:3、在选项中,选择“高级
-
共享文件夹中excel用HEYPERLINK函详细阅读

excel里超链接 链接到本地图片,把表格发给别人时别人打不开,有没有详细的具体操作该怎么解决?这是因为超链接指定的是自己电脑上的路径,在其他电脑中无法定位。将其放到同一个文
-
两个不同的反比例函数的图象能否相详细阅读

两个不同的反比例函数的图像是否会相交,为什么两个不同的反比例函数的图像不会相交。 设两个反比例函数分别为Y1=K1/X1,Y2=K2/X2因为是不同的反比例函数,所以K1与K2不相等; 相
-
python中为什么用了isalpha函数后详细阅读

当汉字和字母混合时,python中的isalpha()出错???求解答!print([d for d in str if not d.isalpha()]) 一般不在遍历列表的时候删除元素,会导致索引出错,可以采用上面这种方法请问C
-
几个多条件计数函数相加的和,只有其详细阅读

EXCEL countif 满足多个条件其中一个即可1、假设“某个单元格”在A1:A5,在A6中进行统计,则公式为: =COUNTIF($A$1:$A$5,0)+COUNTIF($A$1:$A$5,2) 2、如果仅仅指一个单元格如A1,
-
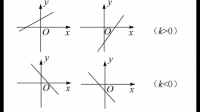
求求高人,有高人出现么。求一次函数详细阅读
一次函数解析式有哪些求法用待定系数法求一次函数的解析式:待定系数法:先设待求函数关系式(其中含有未知常数,系数),再根据条件列出方程或方程组,求出未知系数,从而得到所求结果的方
