信号当中单位阶跃响应和单位序列响应在z域怎么转换

信号与系统阶跃响应的稳态响应怎么求？

首先我们必须明白时域法是直接在时间域上对系统进行分析的方法，具有直观、准确的优点，它可以提供系统时间相应的全部信息。（该方法是最基本的方法，该方法引出的概念、方法、结论都是以后学习复域法、频域法等的基础） 控制系统的性能指标分为动态性能指标和静态性能指标。 在引入典型输入信号的原因是：控制系统的输入信号具有随机性，而如果在这个瞬态上获得系统的解析表达式，难以做到，因此希望有一些特殊的输入信号，通过这些输入信号以及其响应是一个非常不错的选择。 3.1 1、典型的输入信号 ① 单位阶跃信号 对应的输出：单位阶跃响应 一般形式的阶跃函数： 当A=1时，则为单位阶跃函数 ②单位斜坡信号 对应的输出：单

信号与系统的z变换中，知道阶跃响应G（z），如何求出冲激响应H（z）

先求g(k)，差分的单位冲激序列&(k)，再作z变换的H(z). 应该没有直接公式。

在自动控制中单位阶跃函数怎样转换成单位阶跃响应

没法转换。 已知传递函数G，求系统在单位阶跃信号输入下的时间响应方法： y(s)=G(s)*1/s，部分分式分解，拉普拉斯反变换求y(t)

常数的z变换是什么

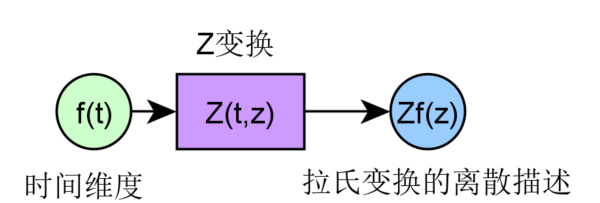
常数的z变换是对离散序列进行的一种数学变换，常用于求线性时不变差分方程的解，它在离散系统中的地位如同拉普拉斯变换在连续系统中的地位。

Z变换（Z-transformation）可将时域信号（即离散时间序列）变换为在复频域的表达式。它在离散时间信号处理中的地位，如同拉普拉斯变换在连续时间信号处理中的地位。

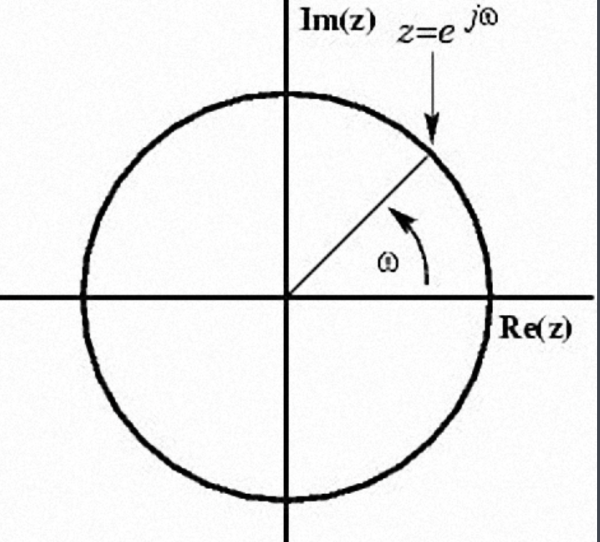
离散时间信号的Z变换是分析线性时不变离散时间系统问题的重要工具，把线性移（时）不变离散系统的时域数学模型——差分方程转换为Z域的代数方程，使离散系统的分析同样得以简化，还可以利用系统函数来分析系统的时域特性、频率响应及稳定性等。

Z变换具有许多重要的特性：如线性、时移性、微分性、序列卷积特性和复卷积定理等等。这些性质在解决信号处理问题时都具有重要的作用。其中最具有典型意义的是卷积特性。由于信号处理的任务是将输入信号序列经过某个（或一系列各种）系统的处理后输出所需要的信号序列，因此，首要的问题是如何由输入信号和所使用的系统的特性求得输出信号。

通过理论分析可知，若直接在时域中求解，则由于输出信号序列等于输入信号序列与所用系统的单位抽样响应序列的卷积和，故为求输出信号，必须进行繁琐的求卷积和的运算。而利用Z变换的卷积特性则可将这一过程大大简化。只要先分别求出输入信号序列及系统的单位抽样响应序列的Z变换，然后再求出二者乘积的反变换即可得到输出信号序列。

这里的反变换即逆Z变换，是由信号序列的Z变换反回去求原信号序列的变换方式。

当前，已有现成的与拉氏变换表类似的Z表。对于一般的信号序列，均可以由表上直接查出其Z变换。相应地，当然也可由信号序列的Z变换查出原信号序列，从而使求取信号序列的Z变换较为简便易行。

单位阶跃响应与单位冲激响应的区别与联系

单位阶跃响应与单位冲激响应：激信号的积分，应用形式，区别和联系具体见以下描述

一、激信号的积分不同：

1、单位阶跃响应为单位冲击响应的积分，单位冲激响应是指在输入为单位冲激信号时系统给出是响应。

2、单位阶跃响应是指在输入信号为单位阶跃信号时系统给出的响应，从输入看单位阶跃信号为单位冲激信号的积分，所以对于同一系统，其各自的响应也是积分关系。

二、应用形式不同：

1、由于输入信号与系统函数满足卷积运算的形式，而单位冲激信号卷积其它函数就等于函数本身。

2、所以单位冲激响应对于研究系统的系统函数、特征函数有重要的意义；单位阶跃响应则可以用来研究系统的响应时间、响应速度等特性。

三、单位阶跃响应与单位冲激响应的联系：

1、符号而已，约定俗成 单位冲击响应是有单位冲激信号引起的响应 单位冲击信号是在某个时刻（实际上是在极短的时间内）有瞬时值。

2、其他时间段内都为0的信号，作用时间积分（求极限）后为1单位脉冲响应是由单位脉冲信号引起的响应。

扩展资料：

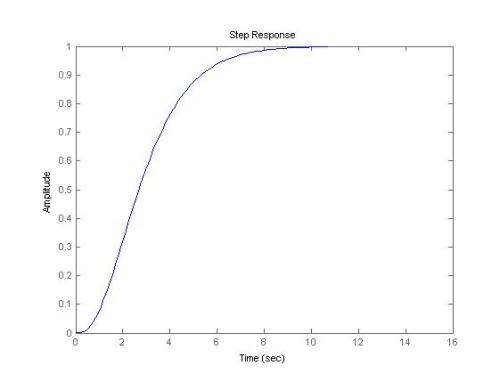
单位阶跃响应：系统动态性能分析

动态性能是系统性能的一个十分重要的指标，通常用阶跃信号作用来测定系统的动态性能。

一般认为，阶跃信号对于系统来说是十分严峻的工作状态，因为阶跃信号中存在跃断点（不连续点）。

针对零初始状态系统在单位阶跃输入下的响应情况，定义了一系列动态性能指标，用以评判系统的动态性能，如超调量、衰减比、上升时间、调节时间、峰值时间等等。

单位冲激响应：应用定义

系统在单位冲激函数激励下引起的零状态响应被称之为该系统的“冲激响应”。它与系统的传递函数互为傅里叶变换关系。

在连续时间系统中，任一个信号可以分解为具有不同时延的冲激信号的叠加。进行实际分析是，可通过电路分析法求解微分方程或采用解卷积的方法，计算出系统的冲激响应。

参考资料来源：百度百科-单位阶跃响应

参考资料来源：百度百科-冲激响应

标签：阶跃响应 计算机 电脑网络 理工学科 硬件