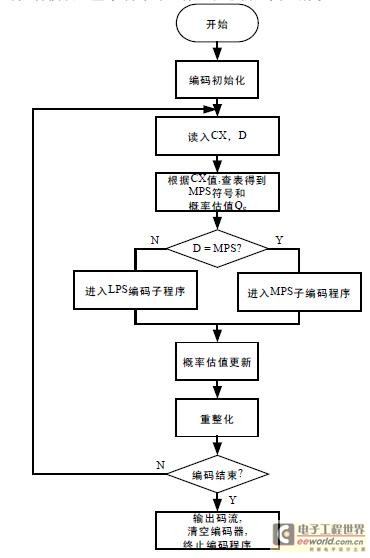
算术编码压缩字符串，精度限制

软件 2024-12-19

算术编码的解码问题

给你几点思路： 1：所谓的编码解码可以约看于压缩和解压缩，无论是哪种编码方式，都不可能是对所有字串或者关键串全部通过一组运算来得到key的？首先这已经是一种，无论从运算量、时间量、空间量都不允许这样做，好比如你要求计算机计算两位数乘两位数，这样的要求还是绝对可以完成的，但是要求几千位数同时乘几千位数，那计算机怎么乘？怎么运算？现在的cpu包括所谓4核的芯，都不可能出现能实现这个要求的指令，而答案必然是分组分部计算，不可能同时运算的。 2：结合第一点的结论，也就是你再算术编码的时候的运算公式是什么，然后你得人为的把它拆分，让字串能每读取一部分的串通过运算累加后也能得到结果。通过这一步骤你不需

简述算术编码需要注意的问题

算数编码的原理我个人感觉其实并不太容易用三言两语直观地表达出来，其背后的数学思想则更是深刻。当然在这里我还是尽可能地将它表述，并着重结合例子来详细讲解它的原理。

简单来说，算数编码做了这样一件事情：假设有一段数据需要编码，统计里面所有的字符和出现的次数。

将区间 [0,1) 连续划分成多个子区间，每个子区间代表一个上述字符，区间的大小正比于这个字符在文中出现的概率p。概率越大，则区间越大。所有的子区间加起来正好是 [0,1)。

编码从一个初始区间 [0,1) 开始，设置:low = 0，high = 1low=0，high=1 不断读入原始数据的字符，找到这个字符所在的区间，比如 [ L, H )，更新: low = low + (high - low) * L \\\ high = low + (high - low) * Hlow=low+(high−low)∗L high=low+(high−low)∗H 最后将得到的区间 [low, high)中任意一个小数以二进制形式输出即得到编码的数据。

乍一看这些数学和公式很难给人直观理解，所以我们还是看例子。例如有一段非常简单的原始数据：ARBER统计它们出现的次数和概率： Symbol Times P A 1 0.2 B 1 0.2 E 1 0.2 R 2 0.4 将这几个字符的区间在 [0，1) 上按照概率大小连续一字排开，我们得到一个划分好的 [0，1)区间。

开始编码，初始区间是 [0，1)。注意这里又用了区间这个词，不过这个区间不同于上面代表各个字符的概率区间[0，1)。这里我们可以称之为编码区间，这个区间是会变化的，确切来说是不断变小。

什么是信源在允许一定失真的条件下，信源熵所能压缩的极限

1．统计编码原理──信息量和信息熵根据香农信息论的原理，最佳的数据压缩方法的理论极限是信息熵。如果要求在编码过程中不丢失信息量，即要求保存信息熵，这种信息保持的编码又叫熵保存编码，或叫熵编码。熵编码是无失真压缩。当然在考虑人眼失真不易察觉的生理特性时，有些图像编码不严格要求熵保存，信息允许通过部分损失来换取高的数据压缩比。这种编码属于有失真数据压缩。信息是用不确定性的量度定义的，也就是说信息被假设为由一系列的随机变量所代表，它们往往用随机出现的符号来表示。我们称输出这些符号的源为“信源”。也就是要进行研究与压缩的对象。信息量信息量指从N个相等可能事件中选出一个事件所需要的信息度量或含量

数据压缩

数据压缩技术主要研究数据的表示、传输和转换方法，目的是减少数据所占据的存储空间和缩短数据传输时所需要的时间。

衡量数据压缩的3个主要指标：一是压缩前后所需的信息存储量之比要大；二是实现压缩的算法要简单，压缩、解压缩速度快，要尽可能做到实时压缩和解压缩；三是恢复效果要好，要尽可能完全恢复原始数据。

数据压缩主要应用于两个方面。一是传输：通过压缩发送端的原始数据，并在接收端进行解压恢复，可以有效地减少传输时间和增加信道带宽。二是存储：在存储时压缩原始数据，在使用时进行解压，可大大提高存储介质的存储量。

数据压缩按照压缩的失真度分成两种类型：一种叫作无损压缩，另一种叫作有损压缩。

无损压缩是指使用压缩后的数据进行重构（或者叫作还原、解压缩），重构后的数据与原来的数据完全相同；无损压缩用于要求重构的信号与原始信号完全一致的场合。一个很常见的例子是磁盘文件的压缩。根据目前的技术水平，无损压缩算法一般可以把普通文件的数据压缩到原来的1/4～1/2。一些常用的无损压缩算法有霍夫曼（Huffman）算法、算术算法、游程算法和LZW（Lenpel-Ziv ＆ Welch）压缩算法。

1）霍夫曼算法属于统计式压缩方法，其原理是根据原始数据符号发生的概率进行编码。在原始数据中出现概率越高的符合，相应的码长越短，出现概率越少的符合，其码长越长。从而达到用尽可能少的符号来表示原始数据，实现对数据的压缩。

2）算术算法是基于统计原理，无损压缩效率最高的算法。即将整段要压缩的数据映射到一段实数半封闭的范围［0，1）内的某一区段。该区段的范围或宽度等于该段信息概率。即是所有使用在该信息内的符号出现概率全部相乘后的概率值。当要被编码的信息越来越长时，用来代表该信息的区段就会越来越窄，用来表示这个区段的位就会增加。

3）游程算法是针对一些文本数据特点所设计的压缩方法。主要是去除文本中的冗余字符或字节中的冗余位，从而达到减少数据文件所占的存储空间。压缩处理流程类似于空白压缩，区别是在压缩指示字符之后加上一个字符，用于表明压缩对象，随后是该字符的重复次数。本算法具有局限性，很少单独使用，多与其他算法配合使用。

4）LZW算法的原理是用字典词条的编码代替在压缩数据中的字符串。因此字典中的词条越多，压缩率越高，加大字典的容量可以提高压缩率。字典的容量受计算机的内存限制。

有损压缩是指使用压缩后的数据进行重构，重构后的数据与原来的数据有所不同，但不影响人对原始资料表达的信息造成误解。有损压缩适用于重构信号不一定非要和原始信号完全相同的场合。例如，图像和声音的压缩就可以采用有损压缩，因为其中包含的数据往往多于我们的视觉系统和听觉系统所能接收的信息，丢掉一些数据而不至于对声音或者图像所表达的意思产生误解，但可大大提高压缩比。

算术编码的工作原理

在给定符号集和符号概率的情况下，算术编码可以给出接近最优的编码结果。使用算术编码的压缩算法通常先要对输入符号的概率进行估计，然后再编码。这个估计越准，编码结果就越接近最优的结果。
例: 对一个简单的信号源进行观察，得到的统计模型如下：
60% 的机会出现符号中性
20% 的机会出现符号阳性
10% 的机会出现符号阴性
10% 的机会出现符号数据结束符. (出现这个符号的意思是该信号源'内部中止'，在进行数据压缩时这样的情况是很常见的。当第一次也是唯一的一次看到这个符号时，解码器就知道整个信号流都被解码完成了。)
算术编码可以处理的例子不止是这种只有四种符号的情况，更复杂的情况也可以处理，包括高阶的情况。所谓高阶的情况是指当前符号出现的概率受之前出现符号的影响，这时候之前出现的符号，也被称为上下文。比如在英文文档编码的时候，例如，在字母Q或者q出现之后，字母u出现的概率就大大提高了。这种模型还可以进行自适应的变化，即在某种上下文下出现的概率分布的估计随着每次这种上下文出现时的符号而自适应更新，从而更加符合实际的概率分布。不管编码器使用怎样的模型，解码器也必须使用同样的模型。
编码过程的每一步，除了最后一步，都是相同的。编码器通常需要考虑下面三种数据：
下一个要编码的符号
当前的区间(在编第一个符号之前，这个区间是[0,1), 但是之后每次编码区间都会变化)
编码器将当前的区间分成若干子区间，每个子区间的长度与当前上下文下可能出现的对应符号的概率成正比。当前要编码的符号对应的子区间成为在下一步编码中的初始区间。
例: 对于前面提出的4符号模型:
中性对应的区间是 [0, 0.6)
阳性对应的区间是 [0.6, 0.8)
阴性对应的区间是 [0.8, 0.9)
数据结束符对应的区间是 [0.9, 1)
当所有的符号都编码完毕，最终得到的结果区间即唯一的确定了已编码的符号序列。任何人使用该区间和使用的模型参数即可以解码重建得到该符号序列。
实际上我们并不需要传输最后的结果区间，实际上，我们只需要传输该区间中的一个小数即可。在实用中，只要传输足够的该小数足够的位数(不论几进制)，以保证以这些位数开头的所有小数都位于结果区间就可以了。
例: 下面对使用前面提到的4符号模型进行编码的一段信息进行解码。编码的结果是0.538(为了容易理解，这里使用十进制而不是二进制；我们也假设我们得到的结果的位数恰好够我们解码。下面会讨论这两个问题)。
像编码器所作的那样我们从区间[0,1)开始，使用相同的模型，我们将它分成编码器所必需的四个子区间。分数0.538落在NEUTRAL坐在的子区间[0,0.6)；这向我们提示编码器所读的第一个符号必然是NEUTRAL，这样我们就可以将它作为消息的第一个符号记下来。
然后我们将区间[0,0.6)分成子区间：
中性的区间是 [0, 0.36) -- [0, 0.6) 的 60%
阳性的区间是 [0.36, 0.48) -- [0, 0.6) 的 20%
阴性的区间是 [0.48, 0.54) -- [0, 0.6) 的 10%
数据结束符的区间是 [0.54, 0.6). -- [0, 0.6) 的 10%
我们的分数 .538 在 [0.48, 0.54) 区间；所以消息的第二个符号一定是NEGATIVE。
我们再一次将当前区间划分成子区间：
中性的区间是 [0.48, 0.516)
阳性的区间是 [0.516, 0.528)
阴性的区间是 [0.528, 0.534)
数据结束符的区间是 [0.534, 0.540).
我们的分数 .538 落在符号 END-OF-DATA 的区间；所以，这一定是下一个符号。由于它也是内部的结束符号，这也就意味着编码已经结束。（如果数据流没有内部结束，我们需要从其它的途径知道数据流在何处结束——否则我们将永远将解码进行下去，错误地将不属于实际编码生成的数据读进来。）
同样的消息能够使用同样短的分数来编码实现如 .534、.535、.536、.537或者是.539，这表明使用十进制而不是二进制会带来效率的降低。这是正确的是因为三位十进制数据能够表达的信息内容大约是9.966位；我们也能够将同样的信息使用二进制分数表示为.10001010（等同于0.5390625），它仅需8位。这稍稍大于信息内容本身或者消息的信息熵，大概是概率为0.6%的 7.361位信息熵。（注意最后一个0必须在二进制分数中表示，否则消息将会变得不确定起来。）