怎么理解二进制二进制,是计算技术中广泛采用的一种数制,由德国数理哲学大师莱布尼茨于1679年发明。二进制数据是用0和1两个数码来表示的数。它的基数为2,进位规则是“逢二进一
复变函数的函数解答 急急急急急急
急!急急!复变函数求大神解答
u=y^2, v=-x^2 实部和虚部分离 ux=0,uy=2y,vx=-2x,vy=0 实部和虚部分别对两个自变量的偏导数 令ux=vy uy=-vx得到y=x 柯西黎曼方程 也就是说f(z)的可导点的集合是L={x+iy|x=y} 可以看出L是一条直线,因此其上任何一点的邻域内总有f(z)的奇点,因此f(z)没有解析点 f'(1+i)=ux+iuy=0+i*2*1=2i复变函数,高手解答啊
∮1/(z+i)*(z+2)dz 你们学过留数定理了没,用留数很好算 因为c为正向圆|z|=3,所以被积函数f(x)=1/(z+i)*(z+2)的奇点为-i,-2,均在圆内 所以∮1/(z+i)*(z+2)dz=2πi(Res[f(z),-i]+Res[f(z),-2]) Res[f(z),-i]=1/(-i+2) Res[f(z),-2]=1/(-2+i) 2πi(Res[f(z),-i]+Res[f(z),-2])=0 原式=0复变函数解析
利用柯西-黎曼方程来求解。
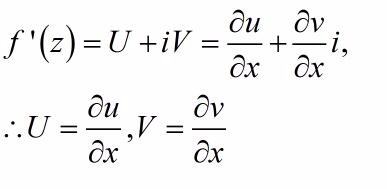
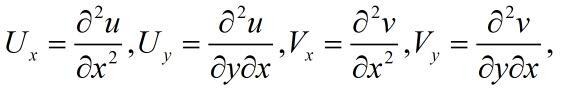
根据柯西-黎曼方程,得到
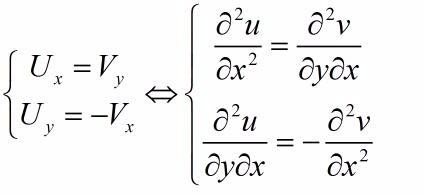
下面再对上式进行化简。
因为f'(z)是某个函数的导函数,又因为
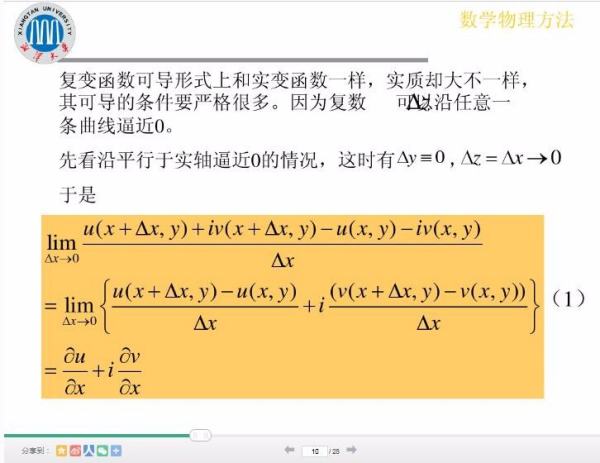
因此在满足可导的条件下,u+iv是f'(z)的一个原函数。因此可以建立柯西-黎曼方程:
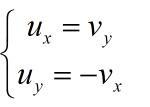
所以
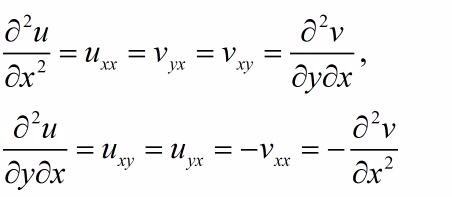
也就是说,只要u和v满足柯西-黎曼方程,U和V就自然满足柯西-黎曼方程。
进而言之,只要f(z)在区域D内解析,其导函数就自然在区域D内解析。反之亦然。
因此f'(z)在区域D内解析的充要条件就是f(z)在区域D内解析,或者说u和v在D内满足柯西-黎曼方程。
关于复变函数的几个问题,急求各位大大们解答!!!!
学习复变函数需要有微积分的基础,除了微分、积分之外,复变函数与高等数学中的曲线积分、无穷级数有特别紧密的联系。 \r\n一个复变函数相当于两个二元函数,但又与研究两个独立的二元函数不同,因为作为初等复变函数的实部与虚部的两个二元函数,在它们的定义区域内,总是满足柯西-黎曼条件的(有点类似曲线积分里积分与路径无关的那样的条件),这就使得复变函数具有不同于实变函数的美好性质,例如复变函数只要有导数,就一定无穷次可导等等。 \r\n复变函数的概念学习可能会比实变函数的概念学习困难些,但只要学会了概念,复变函数里的题目要比实变函数里的题目容易解决。 \r\n就讲这些吧,以后有具体的问题再谈吧。求大神解答复变函数题目
选B。本性奇点
当z->1时,f(z)的极限不存在,且不为∞。在0<|z-1|<+∞环域内将该函数展开成洛朗级数
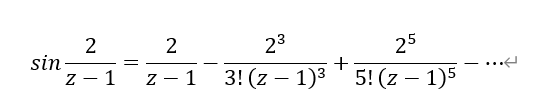
可见,上式有无穷多个(z-1)的负幂项。所以z=1是该函数的本性奇点。
标签:数学 高等数学(大学课程) 大学课程 课程 学习
相关文章
- 详细阅读
-
软件开发如何开始学习详细阅读

软件开发如何开始学习?首先挑选一个方向,学习语言基础,比如C语言,JAVA语言,C#语言,python语言等等,都可以。然后学习写一些简单的小例子,在学习一些网络、通信、存储、数据结构等等
-
企业移动学习推荐哪一家学习比较好详细阅读

企业移动学习平台推荐,哪一家学习平台比较好?想要知道哪一家企业移动学习平台比较好,就要弄清楚一个好的移动学习平台应该是什么样的。作为公司的HR,我经过与同行的了解和平台对
- 详细阅读
-
小朱加安装了100兆的电信宽带,他从详细阅读
家庭用电信100M光纤宽带的上行速率和下行速率分别是多少?您好,电信光纤100M带宽上行和和下行比是1:10。所以下行带宽是10MB/S,上行:10MB/10=1MB.上行带宽是1MB/S 100M带宽下载(
- 详细阅读
-
初中毕业可以去学习电脑技术嘛?详细阅读

初中毕业 想学计算机技术 可以吗当然是可以的,你可以进入计算机类的职业中专就读;不过,读个中专,恐难以学到高深的计算机方面技术,除非自己特别努力;建议你能在中专多学点,今后深造
- 详细阅读
-
学习ps ai pr c4d ae 软件专业,选择详细阅读

学PS AI PR要用什么配置的电脑主要使用PS/PR/AI等常用设计软件,学生或者普通视频、图片设计人员稍微多一些,对于这部分人群,如果常用PR的话,建议i5/R5及以上处理器,内存16GB起,固
-
程序员一般都会用什么网站学习课程详细阅读
程序员一般都会用什么网站学习课程啊?求推荐专业又平价的,感谢!1、慕课网 ----------- 简介 ----------- 提供了丰富的移动端开发、php开发、web前端、android开发以及html5等


